펜윅 트리(1차원 펜윅 트리, Fenwick Tree, Binary Indexed Tree)

ary[9] = {3, 5, 6, 2, 9, 10, 4, 7, 8}

위와 같은 1차원 배열이 있다. 해당 배열에서 ary[3]~ary[7] 구간합을 구하고자 한다.
가장 기본적인 코드는 아래와 같이 하나씩 모두 더하는 것이다.

ary[3]~ary[7]의 합 구하기

해당 코드의 시간복잡도는 O(N) 이다.(연산의 수가 M일 경우 O(MN))
펜윅트리를 사용하게 되면 이를 O(logN) 으로 감소시킬 수 있다.
그렇다면 펜윅트리가 무엇인지 알아보자.

1. 펜윅트리란 무엇인가?
펜윅트리는 Binary Indexed Tree, BIT 라고도 하며, 쉽게 말해 구간합을 빠르게 구하기 위한 자료구조이다.

2. 트리만들기(초기화)
입력받은 배열 ary[9] = {3, 5, 6, 2, 9, 10, 4, 7, 8} 를 이용해 펜윅트리를 만들어 보자.
펜윅트리는 아래과 같이 배열을 구성하게 된다.(펜윅트리는 0번 index를 사용하지 않는다.)

Fenwick Tree

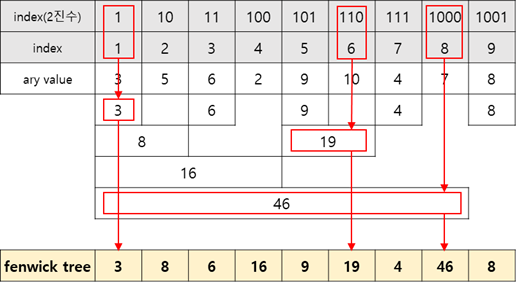
펜윅트리를 확인해 보면, 각각의 index(2진수)에서 가장 뒤에 위치한 1의 값 만큼 자신의 index를 포함하여 그 앞부분 index의 value를 더한다. 1번, 6번, 8번 index를 예로 들어보자.
1번 index의 경우 2진수 값이 1₂ 이므로, 가장 뒤에 위치한 1의 값은 1 이다.
따라서, fenwick tree[1] = ary[1] 이다.
6번 index의 경우 2진수 값이 110₂ 이므로, 가장 뒤에 위치한 1의 값은 2 이다.
따라서, fenwick tree[6] = ary[6] + ary[5] 이다.
8번 index의 경우 2진수 값이 1000₂ 이므로, 가장 뒤에 위치한 1의 값은 8 이다.
따라서, fenwick tree[8] = ary[8] + ary[7] + ... + ary[1] 이다.

2-1. 펜윅트리에서 사용되는 수식
펜윅트리에서는 위와 같이 어떤 값 k를 2진수로 나타냈을 때, 가장 뒤에 위치한 1의 값이 얼마인지 구할 수 있어야 한다.
이를 수식으로 나타내면 다음과 같다.

LB[i] = i & -i ( &는 비트연산, -i = ~i + 1)

LB[i]는 i를 이진수로 나타내었을 때 가장 뒤에 나오는 1이 위치한 값을 구하는 식이다. 예를들어보면 아래와 같다.
LB[3] = 3 & -3 = 11₂ & 01₂ = 1
LB[4] = 4 & -4 = 100₂ & 100₂ = 4
LB[23] = 23 & -23 = 10111₂ & 01001₂ = 00001₂ = 1
LB[56] = 56 & -56 = 111000₂ & 001000₂ = 001000₂ = 8

왜 그런지 간단하게 설명해 보면,
k = 1011000 일 경우, ~k = 0100111 이 된다.
~k+1(-k) 은 ~k의 가장 뒤에 위치한 0이 1로 바뀌며 이 부분이 바로 LB 값이 된다. 그 뒤의 1은 모두 0으로 바뀐다.
(-k = 0101000)
결국, k & -k 를 하게 되면, LB값이 되는 비트만 1이 되고 나머지는 모두 0이 된다.

3. 구간합 구하기
펜윅트리를 이용해 ary[1]~ary[7]의 합을 구하자.

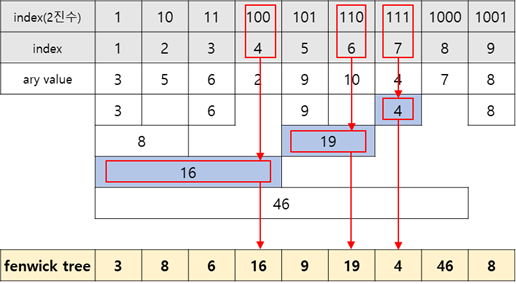
위 그림의 fenwick tree에서 4번, 6번, 7번 index는 아래 수식과 같이, 음영이 칠해진 부분의 값을 의미한다.
f.tree[4] = ary[1]+ary[2]+ary[3]+ary[4]
f.tree[6] = ary[5]+ary[6]
f.tree[7] = ary[7]
이를 통해 구하고자 하는 ary[1]~ary[7]의 합을 구할 수 있다.

이 때, 7=111₂, 6=110₂, 4=100₂ 이며, 가장 마지막에 위치한 1 비트가 0으로 바뀌고 있음을 알 수 있다.
즉, ary[1]~ary[7] = f.tree[111₂]+f.tree[110₂]+f.tree[100₂] 이 된다.
이는, 펜윅트리를 초기화 할 때 가장 마지막 비트의 숫자 만큼을 더하는 과정을 거쳤기 때문에 가능하다.(1. 트리만들기 부분 참고)

이를 통해 일반화한 코드를 작성하면 다음과 같다.(tree는 fenwick tree를, i는 index를 의미)
해당 코드에서는 가장 마지막에 위치한 1 비트를 확인하는 수식(LB[i] = i & -i)을 사용하고 있다.

펜윅트리 합 구하기

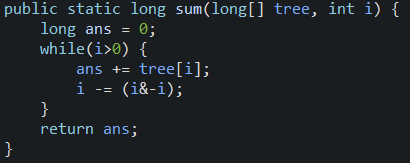
이를 통해 ary[3]~ary[7]의 합 = sum(tree, 7) - sum(tree, 2) 가 됨을 알 수 있다.

이를 이용해 ary[i]~ary[j]의 합을 구하는 식은 다음과 같이 나타낼 수 있다.

sum(tree, j) - sum(tree, i-1)

4. 트리 업데이트
입력받은 배열에서 특정 값이 변경될 경우, 펜윅트리에서는 이 값을 포함하는 모든 인덱스를 변경해 줘야 한다.

위 그림에서 ary[3]을 6에서 4로 변경해 주었다. 값이 2만큼 감소했으므로 펜위트리에서는 3, 4, 8번 index를 2만큼 감소시킴으로써 업데이트를 완료하였다.
변경한 index 들을 살펴보면, 3=11₂, 4=100₂, 8=1000₂ 임을 알 수 있다. 이는, 마지막에 위치한 1의 값을 더함으로써 구해짐을 확인할 수 있다.
이를 통해 일반화한 코드를 작성하면 다음과 같다.(tree는 fenwick tree를, i는 index를, diff는 변경 후 값과 변경 전 값의 차를 의미)

업데이트 수행하기

참고로, 펜윅트리의 초기화는 update함수를 ary[1]~ary[n] 까지 모두 적용하는 방식으로 진행한다.

5. 문제풀이
백준 2042번(https://www.acmicpc.net/problem/2042) 구간 합 구하기를 펜윅트리를 이용해서 풀어보았다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
	public static void main(String[] args) throws IOException {
		// TODO Auto-generated method stub
		int n, m, k;
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine().trim());
		n = Integer.parseInt(st.nextToken());
		m = Integer.parseInt(st.nextToken());
		k = Integer.parseInt(st.nextToken());
		long[] arr = new long[n+1];
		long[] Tree = new long[n+1];
		for(int i=1;i<=n;i++) {
			arr[i] = Long.parseLong(br.readLine());
			update(Tree, i, arr[i]);
		}

		for(int i=0;i<m+k;i++) {
			st = new StringTokenizer(br.readLine().trim());
			int num = Integer.parseInt(st.nextToken());
			int idx = Integer.parseInt(st.nextToken());
			long val = Long.parseLong(st.nextToken());
			if(num == 1) {
				long _diff = val - arr[idx];
				arr[idx] = val;
				update(Tree, idx, _diff);
			}
			else {
				int end = (int)val;
				System.out.println(sum(Tree,end) - sum(Tree, idx-1));
			}
		}
	}
	
	public static void update(long[] tree, int i, long diff) {
		while(i<tree.length) {
			tree[i] += diff;
			i += (i&-i);
		}
	}
	
	public static long sum(long[] tree, int i) {
		long ans = 0;
		while(i>0) {
			ans += tree[i];
			i -= (i&-i);
		}
		return ans;
	}
}