2차원 펜윅트리 이해하기(2-dimentional Fenwick Tree)

 

펜윅트리는 비트연산을 통해 빠른 시간에 구간합을 구하는 배열 형태의 트리이다.

이 글에서는 2차원 펜윅트리만을 설명하고 있다.

1차원 펜윅트리에 대한 이해가 필요하면 블로그 내 펜윅트리 글(https://uldada.tistory.com/5)을 참고하자.

---

2차원 펜윅트리

우선 2차원 펜윅트리의 Update와 Sum 함수를 보자.

update 함수

 

sum 함수

 

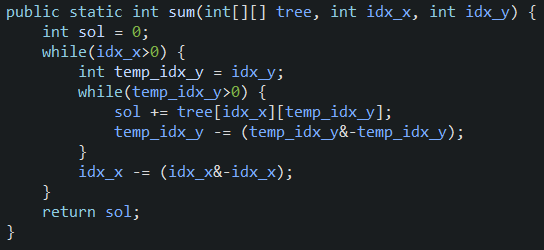
코드를 보면 x축(여기에선 열을 의미)으로 펜윅트리가 동작하며, 그 안에 while문을 통해 y축(행을 의미)으로 펜윅트리가 동작한다.

일단 update를 통해 초기화(입력받은 배열을 통해 펜윅트리 채워나가기)를 진행해 보자 초기화는 update 함수를 통해 진행된다.(1차원 펜윅트리와 동일한 방식)

입력받은 배열은 아래와 같다.

1	2	3	4
5	6	7	8
9	10	11	12
13	14	15	16

첫번째 행부터 채워보자.

다음, 두번째 행을 채워보자.

다음, 세번째, 네번째 행을 바로 채워보자.

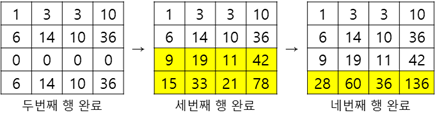
이를 확인해 보면, 오른쪽으로 펜윅트리가 동작함과 동시에, 아래쪽으로도 펜윅트리가 동작한다.

좀 더 구체적으로 설명하면, 아래 그림처럼 오른쪽으로 채워지는 펜윅트리의 각각의 열이 아래쪽으로 채워지고 있다.

1행을 채우는 과정

2행을 채우는 과정

쉽게 말해 while루프 중첩을 통해 오른쪽으로 더해지며, 이 값들이 아래쪽으로 더해지는 것이다.

따라서, sum 함수 또한 위 코드와 같이 while루프 중첩을 통해 합을 구할 수 있는 것이다.

배열에서 (1,1) ~ (3,3) 의 합을 구할 경우 펜윅트리에서 위와 같은 순서로 동작

 

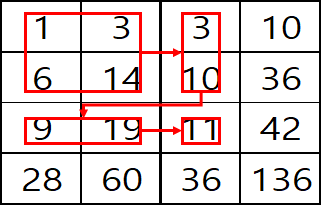
이를 통해 2차원 배열의 구간합을 구할 수 있는데, 방법은 간단하다.

아래와 같이 2차원 배열에서 (x1,y1) ~ (x2,y2) 구간합을 구하고자 한다.

 

이는 펜윅트리에서 아래와 같이 sum함수를 계산함으로써 그 값을 구할 수 있게 된다.

(마찬가지로 x축은 세로, y축은 가로로 설정하였다.)

(x1,y1)~(x2,y2)의 구간합 : sum(x2,y2) – sum(x1-1,y2) – sum(x2,y1-1) + sum(x1-1,y1-1)

 

지금까지 2차원 펜윅트리의 동작방식에 대해 구체적으로 살펴 보았다.

이를 이해한다면 3차원, 4차원 등 고차원 펜윅트리를 만드는 것 또한 쉽게 이해할 수 있을 듯 하다.

백준 11658번 구간 합 구하기 3번을 아래와 같이 풀이하였다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
	public static int[][] matrix;
	public static int[][] tree;
	public static void main(String[] args) throws IOException {
		// TODO Auto-generated method stub
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine().trim());
		int n = Integer.parseInt(st.nextToken());
		int m = Integer.parseInt(st.nextToken());
		matrix = new int[n+1][n+1];
		tree = new int[n+1][n+1];
		
		// Initialize Tree and Matrix
		for(int i=1;i<=n;i++) {
			StringTokenizer st2 = new StringTokenizer(br.readLine().trim());
			int cnt = st2.countTokens();
			for(int j=1;j<=cnt;j++) {
				int val = Integer.parseInt(st2.nextToken());
				matrix[i][j] = val;
				update(tree, i, j, val);
			}
		}

		// Quary solve
		for(int i=0;i<m;i++) {
			StringTokenizer st3 = new StringTokenizer(br.readLine().trim());
			int w = Integer.parseInt(st3.nextToken());
			if(w == 0) {
				int x = Integer.parseInt(st3.nextToken());
				int y = Integer.parseInt(st3.nextToken());
				int c = Integer.parseInt(st3.nextToken());
				int _diff = c-matrix[x][y];
				matrix[x][y] = c;
				update(tree, x, y, _diff);
			}
			else if(w == 1) {
				int x1 = Integer.parseInt(st3.nextToken());
				int y1 = Integer.parseInt(st3.nextToken());
				int x2 = Integer.parseInt(st3.nextToken());
				int y2 = Integer.parseInt(st3.nextToken());
				int ans = sum(tree, x2, y2) - sum(tree, x1-1, y2) - sum(tree, x2, y1-1) + sum(tree, x1-1, y1-1);
				System.out.println(ans);
			}
		}
	}
	
	public static void update(int[][] tree, int idx_x, int idx_y, int diff) {
		while(idx_x<tree.length) {
			int temp_idx_y = idx_y;
			while(temp_idx_y<tree[idx_x].length) {
				tree[idx_x][temp_idx_y] += diff;
				temp_idx_y += (temp_idx_y&-temp_idx_y);
			}
			idx_x += (idx_x&-idx_x);
		}
	}
	
	public static int sum(int[][] tree, int idx_x, int idx_y) {
		int sol = 0;
		while(idx_x>0) {
			int temp_idx_y = idx_y;
			while(temp_idx_y>0) {
				sol += tree[idx_x][temp_idx_y];
				temp_idx_y -= (temp_idx_y&-temp_idx_y);
			}
			idx_x -= (idx_x&-idx_x);
		}
		return sol;
	}
}